Measuring the disclosure risk
A breach of confidentiality occurs when a statistical unit is re-identified and the values of sensitive variables are disclosed. Several approaches have been proposed to measure the disclosure, i.e., re-identifcation risk, but none of them has been universally accepted as the best method.
A quantitative measure of the risk, however, is necessary. Since the disclosure risk cannot be reduced to zero, such a measure would mean adopting a threshold rule to establish whether the release of a dataset is safe. Mathematical measures of the re-identification risk can be classified as:
Mathematical measures of the re-identification risk can be classified as:
- Individual measures, which measure the risk per record. It is typically expressed by means of the probability of correctly re-identifying a unit, or by means of the uniqueness and rareness in the sample or population.
- Global measures, which measure the risk for the entire file. It is typically expressed by means of the expected number of correct re-identifications. Global measures of risk can be derived by synthesizing individual measures.
The advantage of an individual risk measure is that only those records appearing unsafe for a given risk threshold α need to be locally protected, while a global measure involves the protection of the entire file.
Let K be the number of combinations in the population P that is obtained by cross-tabulating a given set of key variables. Denote by k, k=1, …,K a combination of values observed on a sampled unit. Each combination k has its own re-identification risk. All records characterized by the same combination k share the same re-identification risk. Let fk be the frequency count of the records in the sample presenting the same combination k of key variables, and let Fk be the frequency count relative to the same combination k in the population P.
In the following example, we assume that three variables are potential identifiers: sex (M=Male, F=Female), age, and marital status (M=Married; N=Never Married). The file contains 2,500 observations.
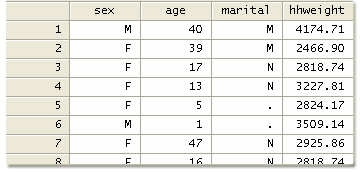
We compute the frequency of each combination of these three variables and obtain the following:
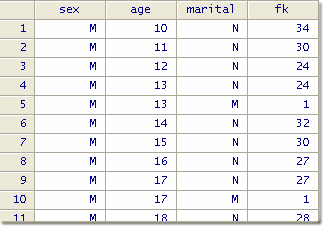
We notice, for example, that the file contains 34 cases of boys, age 10, who have never been married (combination “M / 10 / N”), but only one married boy, age 13 (combination “M / 13 / M”). This combination has a frequency fk of 1, and is thus a sample unique. Since this information comes from a sample survey, we do not know if this combination is also unique in the total population. In other words, Fk is not known and would have to be estimated.
In the sample to be released, only a subset of the total number K of combinations will be observed and only this subset, for which fk> 0 obviously holds, is subject to disclosure risk.
- Sample unique. A record is defined as a sample unique if fk= 1, i.e., there is only one record in the file representing the combination k of scores of the key variables.
- Sample rare. A unit is at risk if fk < α where α is a small integer (usually 3). This rule is referred to as threshold rule or sometime as k-anonymity. Setting a threshold on the sample frequency is quite a conservative approach because re-identification is possible only if the intruder can be confident that a unique/rare unit in the sample is also unique/rare in the population.
- Population unique. A record is defined as a population unique if fk= 1. For census data, or when an administrative register covering the entire population is available, Fk is known for each k and the risk measure can be computed.
- Estimated population unique. For sample surveys, when Fk is unknown for each k, several measures based on inferential procedures (i.e., log linear models) have been proposed.
- Estimated individual risk. Several probabilistic models have been suggested in recent years to estimate the re‑identification risk under an external register scenario. The approach consists of estimating the expected number of re-identifications based on sampling design weights. Due to their features, these methods are suitable for social data sample surveys when the key variables pertain to categorical variables that are often used to define strata in the sampling design phase.
- Record linkage procedure. When key variables are continuous, as is the case with business microdata, a completely different approach to risk measures should be adopted. In fact, the idea of combinations of scores on key variables is meaningless. In this context, every observation might in theory be unique. The concept of rareness in the population could be translated into rareness in the neighborhood of the record, and we should search for outlying observations. One way to measure rareness in the neighborhood is by means of record linkage.
Although all of these measures are individual measures of risk, functions can be derived to transform them into a global measure of disclosure risk for the entire file, for example, by means of the expected number of correct re-identifications in the file. The expected number of re-identifications and the re-identification rate can be obtained as absolute and relative measures of disclosure, respectively.
Note on hierarchical files
Social surveys often collect the same information for each household member, and this information is usually stored in a single record that refers to the household. When defining the re-identification risk, it is important to take into account this dependence among units; indeed, re-identification of an individual in a group may affect the probability of disclosure of all its members. We therefore define the household risk as the probability that at least one individual in the household is re-identified.
